TEOREMA DE PITAGORES

El teorema de pitagores en el seu enunciat habitual estableix que en un triangle rectangue la suma dels quadrats dels catets ( els costats que formen el angle recte ) es igual al cuadrad de la hipotenusa ( l'altre costat ).

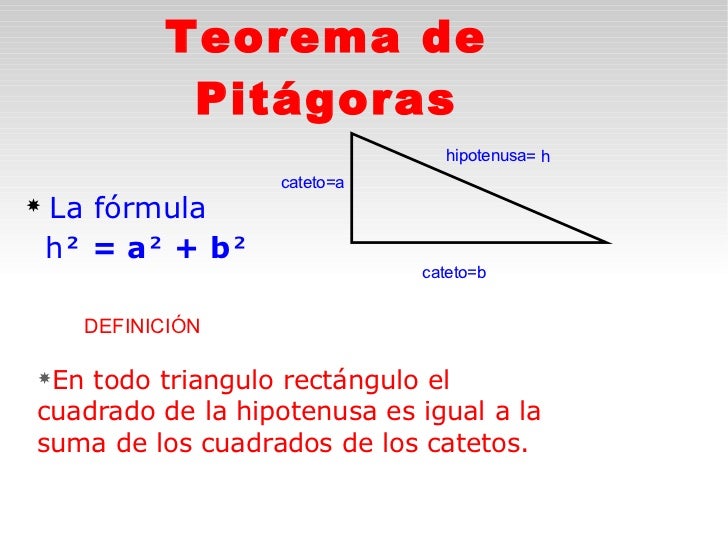
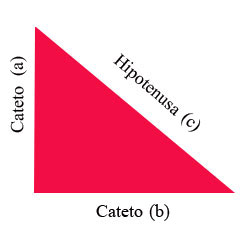
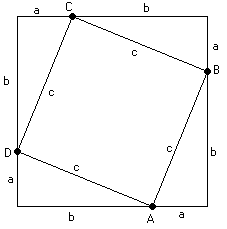
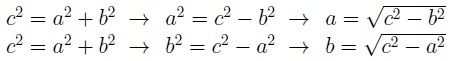El teorema es pot escriure en una equacio :

          

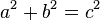
on C representa la longitud de hipotenusa , i A i B representen longituds del altres dos costats.

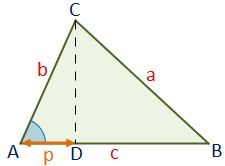
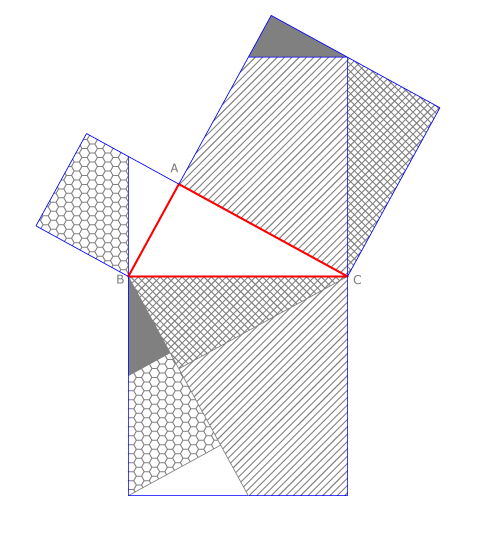
El teorema es refereix tant a les àrees com a les longitudso pot dir-se que a les dues àrees i a les interpretacions mètriques.

                                     

Algunes demostracions del teorema es basen en una interpretació, algunes sobre l'altre, utilitzant tècniques algebraiques i geomètriques. El teorema pot ser generalitzat de diverses maneres, incloent espais de dimensió superior, als espais no euclidians, als objectes que no són triangles rectangles i, de fet, als objectes que no són en tots els triangles, però són n-dimensionals sòlids. El teorema de Pitàgores ha despertat l'interès fora de les matemàtiques com un símbol .

Existen otras ternas pitagoricas :

Teorema De Pitágoras.

El teorema de pitágoras es la relación matemática, de cierta complejidad, más conocida por personas con un formación básica y que ofrece, al mismo tiempo, un importante valor práctico, teórica y didáctico, tanto en su versión aritmético-algebraica como en su version geométrica.

La geometría tiene un papel importante, y por tanto el teorema de Pitágoras no es solo conocido sino también usando ampliamente por los alumnos.

Un triángulo rectángulo el cuadrado del lado más largo (''la hipotenusa'') es igual a la suma de los cuadrados de los otros dos lados (los catetos).

Se establece esta formula: 

                                   




Se pueden construir los dos cuadrados sobre sus catetos (a y b) y el cuadrado sobre la hipotenusa (c). Geométricamente se puede comprobar que cualquier triángulo rectángulo se cumple que la suma de las áreas de los cuadrados formados sobre sus catetos es igual al área del cuadrado constuido sobre la hipotenusa, es decir:















Gracias al teorema de Pitágoras, en un trángulo rectángulo se puede hallar el valor de un cateto sabiendo el otro cateto y la hipotenusa.

Es decir, el valor de un cateto se calcula a partir del otro y la hipotenusa mediante la siguiente fórmula:

El teorema de Pitágoras se puede extender a toda clase de triángulos. El teorema de Pitágoras generalizado relaciona la longitud de los tres lados de un triángulo cualquiera.


Sea p el segmento de la proyencción del lado b sobre el lado c. La fórmula del teorema de Pitágoras generalizado es:






TERNAS PITAGÓRICAS

El conjunto de ternas pitagóricas no tiene fin. Es facil demostralo usando la primera terna pitagórica (3,4 y 5):

Sea n un entero mayor que 1: 3n, 4n y 5n tambien son una terna pitagorica. Esto es verdad porque:

(3n)² + (4n)² = (5n)²               

n	(3n, 4n, 5n)
2	(6,8,10)
3	(9,12,15)
...	... etc ...

Así que puedes crear infinitas ternas pitagóricas a partir de la terna (3,4,5)

JUEGOS DE GUERRA - WAR GAMES

                     

Juegos de guerra (WarGames) es una película estadounidense de 1983, del género thriller, ciencia ficción, dirigida por John Badham.  Protagonizada por Mathew Broderick, Ally Shedy y John Wood en los papeles principales.

El guion está ambientado en los últimos años de la Guerra Fría y cuenta la historia de un joven hacker llamado David que intenta infiltrarse en sistemas ajenos por simple curiosidad.

Un día cenando David ve un anuncio que ha recibido por correo de la empresa Protovisión donde explican que muy pronto sacarán al mercado un juego que revolucionará completamente el universo de los juegos para computador. Evidentemente el objetivo principal de David en la vida se convierte en conseguir conectarse a Protovisión y conseguir jugar al juego antes que nadie.

Al dia siguiente consigue conectarse a lo que parece Protovision pero no consigue deducir el password que le daría acceso al sistema. Solo consigue una lista de juegos entre los que está “El laberinto de Falken”. David investiga la vida de Falken y una noche, junto a Jennifer (amiga de David) deducen que el passaword para entrar al sistema no es otro que el nombre del hijo muerto de Falken (también muerto): Joshua. Descubren un juego de simulación de guerra llamado guerra termonuclear mundial y lo juegan. Se eligen el bando de los rusos para el juego, pero lo que no saben que el juego es real que se han metido en los ordenadores de la base militar rusa.

David se convierte en el heroe de la historia. Reta a Joshua a que juegue contra si mismo al tres en raya (tic-tac-toe) infinitas veces para que se de cuenta de que no todos los juegos se pueden ganar y que no hay diferencia entre ganadores y vencidos.

Teorema de Pitàgores

TEOREMA DE PITÁGORAS 

El otro día en el patio del insituto hicimos como un juego con una cuerda. Nos separamos en tres grupos y cada uno tenia una. Primero la marcamos en 12 partes iguales, bajamos al patio y realizamos la actividad. Consistía en que un miembro del grupo cogía el cable por los dos extremos, otro la cogía por la tercera marca y el otro por la séptima formando el triángulo rectángulo 

Los egipcios utilizaban esta técnica para realizar las parcelas de cultivo iguales y perfectamente rectas, porque cuando subía el nivel del río se borraban y las tenía que volver a hacer. Utilizaban los números 3, 4, 5 para hacer el triángulo rectángulo.

 

Hubieran podido utilizar alguna otra "Terna Pitágora" como por ejemplo: 

( 3 , 4 , 5 )	( 5, 12, 13)	( 7, 24, 25)	( 8, 15, 17)
( 9, 40, 41)	(11, 60, 61)	(12, 35, 37)	(13, 84, 85)
(16, 63, 65)	(20, 21, 29)	(28, 45, 53)	(33, 56, 65)
(36, 77, 85)	(39, 80, 89)	(48, 55, 73)	(65, 72, 97)

El triángulo rectángulo de catetos a y b e hipotenusa c, se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b.

 

Pitágoras de Samo  fue un filósofo y matemático griego considerado el primer matemático puro.
 

 

Teorema de Pitagoras

TEOREMA DE PITAGORAS

El otro día en el patio realizamos una actividad con cuerdas relacionado con el teorema de pitagoras y los egipcios. Nos dividimos en 3 grupos y el primer paso fue marcar un cable en 12 partes iguales, luego bajamos al patio y nos dispusimos a hacer la actividad.

Que consisitia en que un miembro del grupo cogía el cable por los 2 extremos , otro por la 3a marca y el ultimo por la 7a marca, formando un triangulo rectangulo

Esta practica la utilizaban los egipcios para hacer parcelas de cultivo totalmente iguales ya que cuando subia el nivel del río nilo estas quedaban borradas. Utilizaban 3 numeros que eran el 3,4,5 para formar el triangulo rectangulo.

Ellos hubieran podido utilizar otras ternas pitágoricas como:

Y muchos mas ya que las ternas pitágoricas son infinitas.

Teorema de Pitágores

TEOREMA DE PITÀGORES

Els egipcis feien servir el Teorema de Pitàgores antigament antes del naixement d'aquest fent els càlculs en el comerç, per mesurar la Terra i per predir els esdeveniments astronòmics. Aquestes tres necessitats poden ser relacionades en certa forma a la subdivisió àmplia de la matemàtica en l'estudi de l'estructura, l'espai i el canvi.

El mètode egipci que practicàrem en el pati consistia en dividir una corda en 12 parts iguals, sense tallar-la solament marcant-la. La primera persona del grup l'agarrava del primer extrem, la segona del tercer punt, a partir d'eixe punt la tercera persona del grup l'agarra del quart i l'altre extrem que falta l'agarra el primer, formant un triangle rectangle com aquest:


Aquest mètode el feien servir per a medir les zones de Terra, perquè aquest triangle rectangle tenia un angle de 90º i així sabien segur que eren totalment quadrades.

Utilitzaven els nombres naturals, perquè la seva arrel quadrada es exacta o irracional.
Feien trios de nombres especials, anomenats Ternes Pitagòriques que verifiquen el Teorema de Pitàgores amb nombres naturals, exemple: 3,4,5. Ja que 32 + 42 = 52. També són Ternes Pitagòriques els seus múltiples: 6,8,10; 9,12,15...

                            a² + b² = c²

Perfectament podien utilitzar altres Ternes Pitagòriques com per exemple:

( 3 , 4 , 5 )	( 5, 12, 13)	( 7, 24, 25)	( 8, 15, 17)
( 9, 40, 41)	(11, 60, 61)	(12, 35, 37)	(13, 84, 85)

I mes que hi han, perquè existeixen infinits Ternes Pitagòriques.

L'últim teorema de Fermat.

Fermat era un jurista francès del segle XVII conegut com el pare de la teoria de nombres. A través d'un llibre Fermat va començar a estudiar propietats dels nombres, i en aquest llibre ens va deixar la seva afirmació més enigmàtica des de la seva època fins als nostres dies. Per ser l'afirmació de Fermat que més s'ha tractat a demostrar s'anomena últim teorema de Fermat, que era aquest:

És impossible dividir un cub en suma de dos cubs, o biquadrat en suma de dos biquadrats, o en general, qualsevol potència superior a dos en dos potències del mateix grau; he descobert una demostració meravellosa d'aquesta afirmació. Però aquest marge és massa estret per contenir-la.   

Ni més ni menys que 350 anys van haver de passar fins que Andrew Wiles aconseguí demostrar aquest resultat deduint com a corol·lari d'un altre resultat molt més complicat i que, en principi, no tenia res a veure amb el resultat proposat per Fermat. Tenint en compte que Fermat no disposava de totes les eines que va usar Wiles.

teorema de pitàgores

un triangle rectangle, els costats tenen les longituds "3, 4 i 5" però hi han infinites ternes pitagòriques.
El teorema es pot escriure com una equació que relaciona les longituds dels costats a, b, c.

suposats el triangle de catets a i b (formant un angle recte) i la hipotenusa c. Es tracta de demostrar que l'àrea del quadrat de costat c és igual a la suma de les àrees dels quadrats de costat a i costat b.

Si s'afegeixen tres triangles iguals a l'original al voltant del quadrat de costat c formant la figura, s'obté un quadrat. Si la figura central de costat c primerament dibuixada és un quadrat, els seus costats formaran angles rectes, si es gira original 90 graus al voltant dels centre del quadrat, vindrà a ocupar una posició perpendicular a l'original, de mode tal que el costat a serà col·lineal al ccostat b i viceversa, formant-se un quadrat de costat a+b.

El gran quadrat es divideix en un rectangle a l'esquerra i a la dreta. Un triangle es construeix en la meitat de l'àrea del rectangle de l'esquerra. A continuació, es construeix un altre triangle que té la meitat de la zona del quadrat a l'esquerra. Aquests dos triangles han de ser congruents, el que demostra que aquest quadrat té la mateixa àrea que el rectangle de l'esquerra. Si es posen els dos rectangles junts per reformar el quadrat de la hipotenusa en dos rectangles, cadascun amb la mateixa superfície que un dels dos quadrats de les potes.

Al voltant de l'any 400 semblen indicar que Euclides no hauria fet més que transcriure una demostració més antiga que Procle atribueix  a Pitàgores. Tanmateix les proves històriques de la vida de Pitàgores són tan rares que no se li pot atribuir amb certesa la paternitat d'aquesta demostració.

 

Juegos de guerra(War Games)

ARGUMENTO:

La película empieza en una gélida base de misiles donde dos militares son sometidos a una prueba de estrés en la que se verán obligados a decidir si dan la vuelta o no a la llave que condenaría a la muerte segura a millones de personas (comunistas pero personas al fin y al cabo).

La prueba resulta ser un desastre y uno de ellos falla pese a la presión del otro.

resumen se la pelicula (war games)

WarGames, dirigida por John Badham responsable de taquillazos de la talla de Saturday Night Fever (1977), es una cinta clásica de cine de guerra fría con un estilo marcadamente ochentero, donde vemos a un muy joven Matthew Broderick de protagonista.

La historia recuerda a muchos eventos donde el error humano y el informático pudieron desencadenar una hecatombe, por ejemplo, 9 de noviembre de 1979, los ordenadores del NORAD en Monte Cheyenne, el Mando Nacional Militar del Pentágono y el Mando Alternativo Nacional Militar en Fort Ritchie (Maryland) notificaron de la puesta en marcha de un ataque nuclear de categoría MAO-3 procedente de la Unión Soviética.

Esto puso en alerta a todo el aparato nuclear de los Estados Unidos, pero finalmente se desecho la orden de contraataque, al considerarse que no había evidencias reales de tal ataque, pese a que los ordenadores mostraban los impacto de centenares de misiles.

Finalmente todo era producto de las instrucciones erróneamente introducidas a los ordenadores que simularon un ataque nuclear. En el Pentagono hubo un tiempo en que las respuestas nucleares quisieron dejarse en manos de un ordenador, especialmente de los silos de lanzamiento, debido supuestamente a que al menos un 50% de los operadores de los lanzamientos se negaban a disparar recibida la orden.

Teorema de Pitágoras

Teorema de Pitágoras

El Teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa(el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos(los dos lados menores del triángulo, los que conforman el ángulo recto).

                          
                a² + b² = c²


El teorema de Pitágoras tiene este nombre porque su descubrimiento recae sobre la escuela pitagórica. Anteriormente, en Mesopotámia y el antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefren, datada en el s. XXVI a.C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.

El teorema de Pitágoras es de los que cuenta con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de "Magíster matheseos".

Se estima que se demostró el teorema mediante semejanza de triángulos: sus lados homólogos son proporcionales.¹

Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a’ y b’, proyecciones en ella de los catetos a y b, respectivamente.

Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.

teorema de pitagores jaume soler

	En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de loscatetos. a2 + b2 = c2
Cada uno de los sumandos, representa el área de un cuadrado de lado, a, b, c. Con lo que la expresión anterior, en términos de áreas se expresa en la forma siguiente:
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

Teorema de Pitágoras generalizado

Si en vez de construir un cuadrado, sobre cada uno de los lados de un triángulo rectángulo, construimos otra figura, ¿seguirá siendo cierto, que el área de la figura construida sobre la hipotenusa es igual a la suma de las áreas de las figuras semejantes construidas sobre los catetos?

(Pinchando en los dibujos siguientes se accede a la comprobación numérica en las figuras que se representan)

DEMOSTRACIONES DEL TEOREMA DE PITÁGORAS
A lo largo de la historia han sido muchas las demostraciones y pruebas que matemáticos y amantes de las matemáticas han dado sobre este teorema. Se reproducen a continuación algunas de las más conocidas.

DEMOSTRACIONES GEOMÉTRICAS

PITÁGORAS.

Una de las demostraciones geométricas mas conocidas, es la que se muestra a continuación, que suele atribuirse al propio Pitágoras. A partir de la igualdad de los triángulos rectángulos es evidente la igualdad a2 + b2 = c2

PLATÓN.

La relación que expresa el teorema de Pitágoras es especialmente intuitiva si se aplica a un triángulo rectángulo e isósceles. Este problema lo trata Platón en sus famosos diálogos. Hacían servir este método para delimitar otra vez después de de la subida del río Nilo los campos de cultivo que se habían sido destruidos por la subida del rio. Trataban de solucionar el problema de hacer ángulos rectos, utilizaban los números 3,4,5 no podrian hacer otra terna pitagorica porke no las sabian.

Teorema de Pitàgoras.

El Teorema de Pitàgoras  en su enunciado habitual establece que un triangulo rectangulo la suma de los cuadrados de los catetos(los lados que forman el angulo recto)és igual al cuadrado de la hipotenusa.

El recíproc tambien se cumple,és decir: en un triangulo, si la suma de los cuadrados  de las longitudes de los lados mas cortos  és igual al cuadrado de la longitud del lado mas largo , es decir  el angulo comprimido entre los dos lados mas cortos  és un angulo recto.

El teorema se puede escibir  como una equacíon  que relaciona las longitudes e los lados  a, b, i c, se denomina Equacion de Pitàgoras.   donde c representa la longitud de la hipotenusa, i a i b representan  las longitudes de los otros dos lados.



El teorema de Pitàgoras debe el nombre  al matematico griego  Pitàgoras, al que segun la tradición se le  atribulle  su  descubrimiento  i la demostración, todavia sabiendo que se argumenta que el conocimiento de el teorema era  ja anterior.Hai pruebas de que los mtematicos babilonios  conocian la formula , todavia recibimos mui poca información  sobre el uso que hacian.

El teorema se refiere tanto alas àreas  como las longitudes, o puede decirse que las dos àreas y a las interpretaciones matemàticas.Algunas demostraciones  del teoremase basan en una interpretacion , algunas sobre el otro, utilizando tecnicas algebraticas y geometricas. El teorema puede ser generalizado  de diversas maneras, incluyendo espacios de dimenisón superieror,alos espacion no rellenados , a los objetos que no són triangulo rectaàngulos  y, y de echo alos objetos  que no són en todos triangulos, però són n-dimensionales sòlidos. El teorema de Pitàgoras ha despertado el interes fuera de las matematicas como un simbolo de el ermetismo  de las matematicas, de la mística, o el poder intel·lectual; referèncias en laliteratura popular, obras de teatro, abundanlos musicales,canciones,  y en los dibujos animados.