El teorema de pitágoras es la relación matemática, de cierta complejidad, más conocida por personas con un formación básica y que ofrece, al mismo tiempo, un importante valor práctico, teórica y didáctico, tanto en su versión aritmético-algebraica como en su version geométrica.
La geometría tiene un papel importante, y por tanto el teorema de Pitágoras no es solo conocido sino también usando ampliamente por los alumnos.
Un triángulo rectángulo el cuadrado del lado más largo (''la hipotenusa'') es igual a la suma de los cuadrados de los otros dos lados (los catetos).
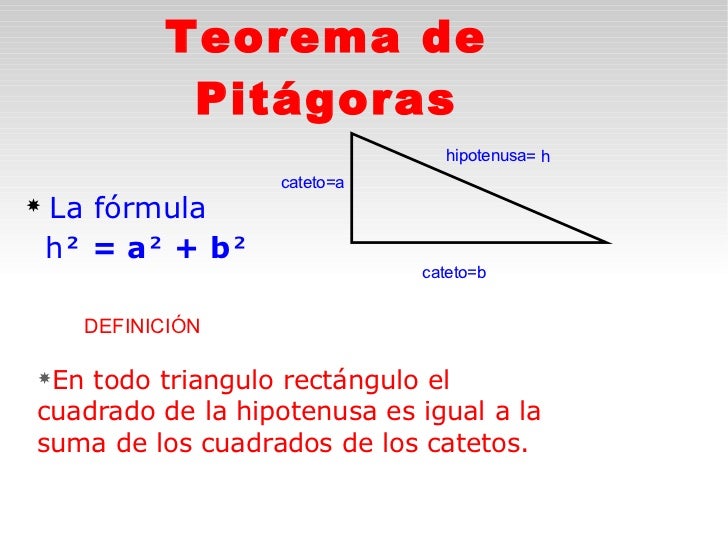Se establece esta formula:
Se establece esta formula: Se pueden construir los dos cuadrados sobre sus catetos (a y b) y el cuadrado sobre la hipotenusa (c). Geométricamente se puede comprobar que cualquier triángulo rectángulo se cumple que la suma de las áreas de los cuadrados formados sobre sus catetos es igual al área del cuadrado constuido sobre la hipotenusa, es decir:
Gracias al teorema de Pitágoras, en un trángulo rectángulo se puede hallar el valor de un cateto sabiendo el otro cateto y la hipotenusa.
Es decir, el valor de un cateto se calcula a partir del otro y la hipotenusa mediante la siguiente fórmula:
El teorema de Pitágoras se puede extender a toda clase de triángulos. El teorema de Pitágoras generalizado relaciona la longitud de los tres lados de un triángulo cualquiera.
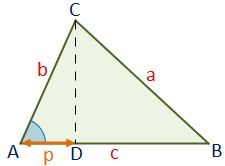
Sea p el segmento de la proyencción del lado b sobre el lado c. La fórmula del teorema de Pitágoras generalizado es:
TERNAS PITAGÓRICAS
El conjunto de ternas pitagóricas no tiene fin. Es facil demostralo usando la primera terna pitagórica (3,4 y 5):
Sea n un entero mayor que 1: 3n, 4n y 5n tambien son una terna pitagorica. Esto es verdad porque:
(3n)2 + (4n)2 = (5n)2
| n | (3n, 4n, 5n) |
|---|---|
| 2 | (6,8,10) |
| 3 | (9,12,15) |
| ... | ... etc ... |
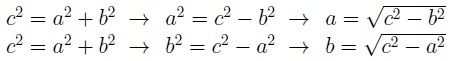
Cap comentari:
Publica un comentari a l'entrada