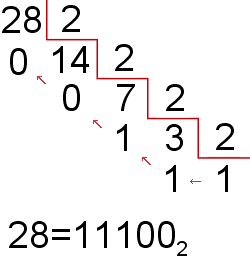Aqui esta mi post del feedly ..
divendres, 28 de novembre del 2014
Sistema solar a escala de tamany
SISTEMA SOLAR A ESCALA DE TAMANYS
Està fet per tamanys però no a distancia de cadascú:
dijous, 27 de novembre del 2014
dimecres, 12 de novembre del 2014
Fita històrica: aterratge mòdul "Philae" sobre cometa 67P/Churyumov–Gerasimenko
La fita històrica de la qual vos he parlat aquest matí és l'aterratge sobre el cometa 67P/Churyumov–Gerasimenko del mòdul Philae, que forma part de la sonda Rosetta.
La sonda Rosetta va ser llançada a l'espai per l'Agència Espacial Europea (ESA) des de la guaiana francesa ara farà uns 10 anys. La sonda porta al seu si un mòdul que serà l'encarregat de descendre sobre el cometa i ancorar-se a ell.
Ací podeu vore un vídeo d'una simulació de l'aterratge:
Aquesta fita històrica té tanta importància fonamentalment per dos motius:
La sonda Rosetta va ser llançada a l'espai per l'Agència Espacial Europea (ESA) des de la guaiana francesa ara farà uns 10 anys. La sonda porta al seu si un mòdul que serà l'encarregat de descendre sobre el cometa i ancorar-se a ell.
Ací podeu vore un vídeo d'una simulació de l'aterratge:
- Pel desafiament tecnològic que comporta: la sonda i el cometa estan a més de 500 milions de kilòmetres de la terra, les senyals de ràdio tarden més de 28 minuts en fer el viatge! A més tot va ser planificat fa 10 anys i tot s'ha de controlar escrupolosament al mil·límetre des d'aquesta distància.
- Pels coneixements científics que s'espera obtenir, sobre l'origen del sistema solar, dels planetes i fins i tot de la vida.
Per a més informació podeu visitar el bloc de la sonda Rosetta (en anglés).
dijous, 6 de novembre del 2014
Paco Ruzafa - Sistema Binari
El sistema binari és un sistema de numeració en el qual tots els nombres es representen utilitzant com base dues xifres: zero i un (0 i 1). En altres paraules, és un sistema de numeració de base 2, mentre que el sistema que utilitzem més habitualment és de base 10, o decimal.
Els ordinadors treballen internament amb dos nivells de voltatge, pel que el seu sistema de numeració natural és el sistema binari (encès, apagat).
Si el sistema decimal treballa amb deu xifres (0,1,2,3,4,5,6,7,8,9), el sistema octal o de base vuit treballaria amb vuit (0,1,2,3,4,5,6,7). El sistema binari, o de base dos, només n'utilitza dos (0 i 1).
dimecres, 5 de novembre del 2014
EXPLICACIO DE BINARI A DECIMAL
! EXPLICACION DE BINARIO ¡
- El sistema binari, anomenat també sistema diádico en ciències de la computació, és un sistema de numeració en el qual els nombres es representen utilitzant solament les xifres zero i un (0 i 1). És un dels que s'utilitza en els ordinadors, ja que treballen internament amb dos nivells de voltatge, per la qual cosa el seu sistema de numeració natural és el sistema binari (encès 1, apagat 0) .
! DECIMAL A BINARI ¡
- Aquesta forma és la més comuna i la que més s'ensenya a la gent que està començant. Consisteix a dividir el nombre decimal per la base binari que és sempre 2, tornarem a repetir entre dos fins que no puguem dividir més.
- A continuació ens fixem en les restes, veiem que la resta de cada divisió en 0 o 1. Ara escrivim les restes de dreta a esquerra, com indica la fletxa de la imatge i escrivim el nombre resultant: 1100100
eixe seria el mètode de pasar de numeros decimals a binaris.
! DE BINARIO A DECIMAL ¡
-En el Sistema Decimal podem escriure nombres com 451, 672, 30, etc. És a dir, podem formar qualsevol combinació dels dígits del 0 al 9 (xifres). En Sistema Binari podem escriure nombres com 01100111, 1110, 011, 1, etc. És a dir, podem formar qualsevol combinació dels dígits 0 i 1 (bits).
sistema de numeracion binario
El sistema binari és un sistema de numeració en el qual tots els nombres es representen utilitzant com base dues xifres: zero i un (0 i 1). En altres paraules, és un sistema de numeració de base 2, mentre que el sistema que utilitzem més habitualment és de base 10, o decimal.
Si el sistema decimal treballa amb deu xifres (0,1,2,3,4,5,6,7,8,9), el sistema octal o de base vuit treballaria amb vuit (0,1,2,3,4,5,6,7). El sistema binari, o de base dos, només n'utilitza dos (0 i 1).
El sistema de numeración decimal incorpora una serie de reglas que permiten representar una serie infinita de números.
Explicacíon del Sistema Binario
El sistema binario, llamado también sistema diádico en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Es uno de los que se utiliza en las computadoras, debido a que trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).
Este video describe un poco al sistema de números binarios y muestra como trasformar números decimales a binarios utilizando una tabla, que de forma simple nos ayuda a esa tarea.
Este video describe un poco al sistema de números binarios y muestra como trasformar números decimales a binarios utilizando una tabla, que de forma simple nos ayuda a esa tarea.
Sistema binario de números
 |
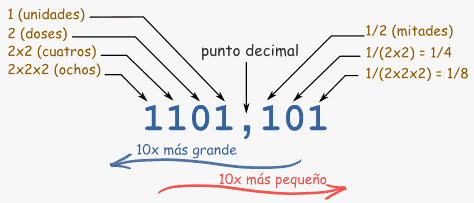| Este número es 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8) (=13,625 en decimal) |
Un número binario sólo tiene ceros y unos.
Alfonso Pérez - Sistema Binari
Hola a todos! Hoy os voy a explicar el sistema binario .
Sistema Decimal podemos escribir números como 451, 672, 30, etc. Es decir,
podemos formar cualquier combinación de los dígitos del 0 al 9 (cifras).
En Sistema Binario podemos escribir números como 01100111, 1110, 011, 1, etc. Es
decir, podemos formar cualquier combinación de los dígitos 0 y 1 (bits).
Cada número en Sistema Decimal tiene su equivalente en Sistema Binario, y viceversa.
Aqui os dejo un video y una imagen de como passar decimal a binario
Y aqui os dejo como hacerlo a la inversa
Sistema de numeració binaria
El sistema binari, en matemàtiques i informàtica, és un sistema de numeració en el qual els nombres es representen utilitzant solament les xifres zero i un (0 i 1). És el que s'utilitza en els ordinadors, ja que treballen internament amb dos nivells de voltatge, pel que el seu sistema de numeració natural és el sistema binari (encès 1, apagat 0).
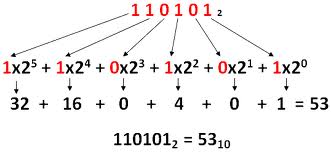
De binari a decimal
En sistema decimal, les xifres que componen un nombre són les quantitats que estan multiplicant a les diferents potències de deu (10, 100, 1000, 10000, etc.)
Per exemple, 745 = 7 · 100 + 4 · 10 + 5 · 1
O el que és el mateix: 745 = 7 · 102 + 4 · 101 + 5 · 100
En el sistema binari, les xifres que componen el nombre multipliquen a les potències de dos (1, 2, 4, 8, 16, ....)
20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64, ...
Per exemple, per passar a binari un nombre decimal, comencem per la dreta i anem multiplicant cada xifra per les successives potències de 2, avançant cap a l'esquerra:
101.102 = 0 · 1 + 1 · 2 + 1 · 4 + 0 · 8 + 1 · 16 = 2 + 4 + 16 = 2210
1102 = 0 · 1 + 1 · 2 + 1 · 4 = 2 + 4 = 610
-----------------------------------------------------------------------------------------------------------------------------
De decimal a binari
Per fer la conversió de decimal a binari, cal anar dividint el nombre decimal entre dos i anotar en una columna a la dreta la resta (un 0 si el resultat de la divisió és parell i un 1 si és imparell).
La llista de zeros i uns llegits de baix a dalt és el resultat.
Exemple: anem a passar a binari 7910
79 1 (imparell). Dividim entre dos:
39 1 (imparell). Dividim entre dos:
Gener 19 (imparell). Dividim entre dos:
Setembre 1 (imparell). Dividim entre dos:
4 0 (parell). Dividim entre dos:
2 0 (parell). Dividim entre dos:
Gener 1 (imparell).
Per tant, 7910 = 10.011.112
Ací teniu una imatge de com pasar de decimal a binari.
 |
Sistema Binari
El sistema binari és un sistema de numeració en el qual tots els nombres es representen utilitzant com base dues xifres: zero i un (0 i 1). En altres paraules, és un sistema de numeració de base 2, mentre que el sistema que utilitzem més habitualment és de base 10, o decimal.
Ací et deixe un vídeo de com es passa un número al codi binari:
Els ordinadors treballen internament amb dos nivells de voltatge, pel que el seu sistema de numeració natural és el sistema binari (encès, apagat).
Si el sistema decimal treballa amb deu xifres (0,1,2,3,4,5,6,7,8,9), el sistema octal o de base vuit treballaria amb vuit (0,1,2,3,4,5,6,7). El sistema binari, o de base dos, només n'utilitza dos (0 i 1).
Ací et deixe un vídeo de com es passa un número al codi binari:
diumenge, 2 de novembre del 2014
Arancha Gil - Sistema binari
Hola amics, ací us deixe el vídeo sobre l'explicació del sistema binari :)
A més, aquí una breu explicació:
Els sistemes de numeració més utilitzats són el decimal i el binari.
A més, aquí una breu explicació:
El conjunt de símbols gràfics que representen xifres i regles i ens permeten expressar i operar amb quantitats, és el que coneixem com a sistema de numeració.
Els sistemes de numeració més utilitzats són el decimal i el binari.
Ambdós sistemes són posicionals: els símbols canvien de valor segons la seva posició en el nombre escrit. El que els diferencia és la seva base.
Subscriure's a:
Missatges (Atom)