
cualquier terna pitagórica se puede asociar con las longitudes de dos catetos y una hipotenusa, formando un triángulo rectángulo.

Las ternas pitagóricas suelen representarse como (a,b,c). Las ternas cuyos tres números son coprimos reciben el nombre de ternas pitagóricas primitivas. Las 16 primeras ternas pitagóricas primitivas, con c ≤ 100 son:
| ( 3 , 4 , 5 ) | ( 5, 12, 13) | ( 7, 24, 25) | ( 8, 15, 17) |
| ( 9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (16, 63, 65) | (20, 21, 29) | (28, 45, 53) | (33, 56, 65) |
| (36, 77, 85) | (39, 80, 89) | (48, 55, 73) | (65, 72, 97) |
Ultimo teorema de Fermat
En teoría de números, el último teorema de Fermat, o teorema de Fermat-Wiles, es uno de los teoremas más famosos en la historia de la matemática. Utilizando la notación moderna, se puede enunciar de la siguiente manera:
El teorema fue conjeturado por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995 por Andrew Wiles ayudado por el matemático Richard Taylor. La búsqueda de una demostración estimuló el desarrollo de la teoría algebraica de números en el siglo XIX y la demostración del teorema de la modularidad en el siglo XX. |
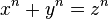
Cap comentari:
Publica un comentari a l'entrada