Haciendo 12 puntos a la misma distancia se coge del extremo de la cuerda, los numeros 3, 4 y 5 ahi que unirlos para que salga un triangulo y asi poder sacar un angulo de 90º. Al igual que existe esta "terna Pitagorica" existen muchas otras para poder sacar distintos angulos y formas geometricas tal como: Estos son los ternos primitivos.(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29)...
Las ternas pitagóricas pueden clasificarse de dos maneras, primitivas o no primitivas. Una terna pitagórica primitiva es aquella en la que el máximo común divisor de a, b y c es 1.
1.En que consistia el mètode egipci que practicàrem al pati?En fer dos lines perpenticulars.
2.Per a què feien servir aquest mètode?Per a fer un angle de 90º
3.Quin era el problema que tractaven de resoldre?Com fer una angle de 90º en un corda i 12 punts
4.Quins nombres utilitzaven? 3,4 i 5 Per què aquests nombres?Perqe son el mes baixets i son els mes facils.
5.Hagueren pogut utilitzar alguna altra "Terna Pitagòrica"?Si Quantes ternes d'aquestes creus que podran existir? Nian infinitat de ternes Pitagoriques (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29)...
El último teorema de Fermat, postulado por Pierre de Fermat alrededor de 1637, plantea que no existen ternas no triviales (como a = b = c = 0 o a = 1, b = 0, c = 1) análogas a las ternas pitagóricas con números naturales, generalizando para exponentes mayores que dos. En notación moderna:
La ecuación:
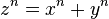no tiene solución si n>2 con x, y, z, n naturales.
Durante más de 300 años, Andrew Wiles consiguió demostrarlo en 1995, utilizando para ello, herramientas matemáticas muy avanzadas.
Teorema de Pitágoras
En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de loscatetos.
Si un triángulo rectángulo tiene catetos de longitudes 
y 
, y la medida de la hipotenusa es 
, se establece que:
y , y la medida de la hipotenusa es , se establece que:(1)
Cap comentari:
Publica un comentari a l'entrada