Codigo Binario:
Sistema binario de números
Un número binario sólo tiene ceros y unos.
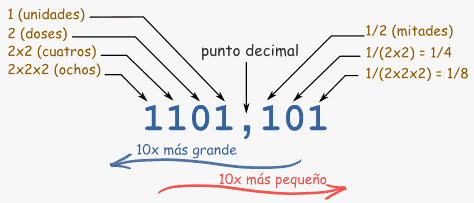 |
Este número es 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8)
(=13,625 en decimal) |
De la misma manera que en el
sistema decimal, se pueden poner números a la izquierda o a la derecha del punto decimal, para indicar valores mayores o menores que uno. En el sistema binario:
 | El número justo a la izquierda del punto es un número entero, lo llamamos unidades.
Cuando vamos a la izquierda, cada posición vale 2 veces más. |
| | |
 | La primera cifra a la derecha del punto significa mitades(1/2).
Cuando vamos a la derecha, cada posición vale 2 veces menos (la mitad de la anterior).
Dos valores diferentes
Como sólo puedes tener ceros y unos, en binario se cuenta así:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|
| Binario: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|
| Decimal: | 20 | 25 | 30 | 40 | 50 | 100 | 200 | 500 |
|---|
| Binario: | 10100 | 11001 | 11110 | 101000 | 110010 | 1100100 | 11001000 | 111110100
|
|---|
Ejemplos
Ejemplo 1: ¿Cuánto es 11112 en decimal?
- El "1" de la izquierda está en la posición "2×2×2", esto es 1×2×2×2 (=8)
- El siguiente "1" está en la posición "2×2", esto es 1×2×2 (=4)
- El siguiente "1" está en la posición "2", esto es 1×2 (=2)
- El último "1" son las unidades, es decir 1
- Respuesta: 1111 = 8+4+2+1 = 15 en decimal
Ejemplo 2: ¿Cuánto es 10012 en decimal?
- El "1" de la izquierda está en la posición "2×2×2", así que vale 1×2×2×2 (=8)
- El "0" siguiente está en la posición "2×2", así que vale 0×2×2 (=0)
- El "0" está en la posición "2", así que vale 0×2 (=0)
- El último "1" son las unidades, así que vale 1
- Respuesta: 1001 = 8+0+0+1 = 9 en decimal
Ejemplo 3: ¿Cuánto es 1,12 en decimal?
- El "1" de la izquierda está en la posición de las unidades, así que vale 1.
- El "1" de la derecha está en la posición de las "mitades", así que vale 1×(1/2)
- Por tanto, 1,1 es igual a "1 y 1 medio" = 1,5 en decimal
Ejemplo 4: ¿Cuánto es 10,112 en decimal?
- El primer "1" está en la posición "2", así que vale 1×2 (=2)
- El "0" está en la posición de las unidades, vale 0
- El "1" a la derecha del punto está en la posición de las "mitades", así que vale 1×(1/2)
- El último "1" está en la posición de los "cuartos", así que vale 1×(1/4)
- Entonces, 10,11 es 2+0+1/2+1/4 = 2,75 en decimal
|

Cap comentari:
Publica un comentari a l'entrada